PERUBAHAN GRAFIK TRIGONOMETRI

Grafik $sin\ x,\ cos\ x,\ atau\ tan\ x$ sudah lumrah kita kenal dan ingat. Akan tetapi bagaimana kalau kita diminta untuk menggambar grafik $y=2sin\ 2(x+45)+1$?. Bagaimana langkah kita menggambar fungsi tersebut? Apakah kita dapat memperoleh grafik tersebut berdasarkan grafik dasar $sin\ x$?. Dalam artikel ini akan dibahas bagaimana cara kita memperoleh grafik tersebut. Sebelum kita menjawab soal tersebut, ada beberapa hal yang harus kalian pahami.

Diketahui fungsi:

$y=Asin\ B(x+\alpha^o )+C$

$y=Acos\ B(x+\alpha^o)+C$

$y=Atan\ B(x+\alpha^o )+C$

❤ Perubahan (A) mempengaruhi amplitudo suatu fungsi. Amplitudo didefinisikan $A=\frac{y_{max}-y_{min}}{2}$.

⃝ Jika (A) isi tanda negatif $(-)$, maka grafik $y=Asin\ B(x+\alpha^o )+C,\ y=Acos\ B(x+\alpha^o )+C$ atau $y=Atan\ B(x+\alpha^o )+C$ dicerminkan terhadap sumbu-(x). Lihat gambar di bawah sebagai contoh.

❤ Perubahan (B) mempengaruhi periode. Untuk $(sin\ Bx)\ atau\ (cos\ Bx)\ mempunyai\ periode=\frac{360^o}{B}$ artinya, sejauh $\frac{360^o}{B}$ menghasilkan satu gelombang. Sedangkan untuk $(tan\ Bx)\ mempunyai\ periode=\frac{180^o}{B}$. Jika (B) negatif $(-)$, maka lihat kembali materi grafik fungsi genap dan fungsi ganjil.

❤ Perubahan $\alpha^o$ mempengaruhi pergeseran grafik $y=Asin\ B(x)$ searah sumbu -(x) yaitu ke kiri maupun ke kanan. Jika $(+\alpha^o)$ grafik akan digeser ke kiri, sedangkan $(-\alpha^o)$  grafik akan digeser ke kanan.

❤ Perubahan (C) mempengaruhi pergeseran grafik $y=Asin\ B(x+\alpha^o)$ atau $y=Acos\ B(x+\alpha^o)$ searah sumbu-(y) yaitu ke atas maupun ke bawah. Jika $(-C)$ grafik di geser ke bawah sejauh (C) sedangkan jika $(+C)$ grafik di geser ke atas sejauh (C).

 

⃞ Sebagai contoh, kita akan menggambar grafik $y=2sin\ 2(x+45^o)+1$

Langkah-langkah menggambar grafik di atas sebagai berikut:

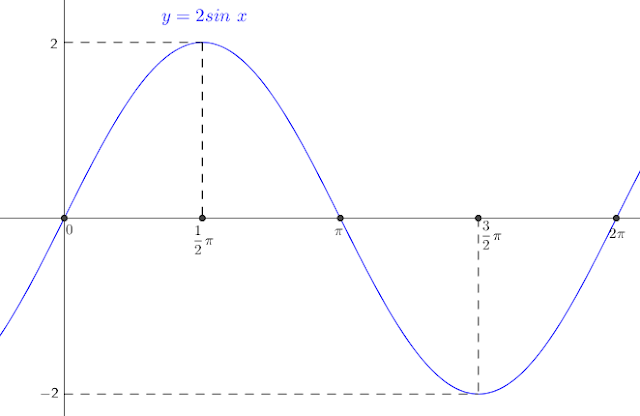
1. Gambar dulu grafik $y=2sin\ x$ dengan amplitudonya 2, di dapat dari $A=\frac{y_{max}-y_{min}}{2}=\frac{2-(-2)}{2}=2$. Gambarnya akan tampak seperti di bawah ini.

2. Gambar grafik $y=2sin\ 2x$ dengan periodenya $periode=\frac{360^o}{2}=180^o$ artinya sejauh (180^o) menghasilkan satu gelombang. Gambarnya akan tampak seperti di bawah ini.

3. Gambar grafik $y=2sin\ 2(x+45^o)$. Dengan penambahan sudut $90^o\Rightarrow y=2sin\ 2(x+45^o)=2sin\ (2x+90^o)$ maka grafik pada langkah-2 di geser ke kiri sejauh (45^o). Gambarnya akan tampak seperti di bawah ini.

4. Gambar grafik $y=2sin\ 2(x+45^o)+1$. Untuk menggambar grafik ini tinggal menggeser grafik pada langkah ke-3 ke atas sejauh 1 satuan. Gambarnya akan tampak seperti di bawah ini.

Untuk menggambar grafik trigonometri yang lain, langkah-langkahnya juga sama seperti di atas.
Lihat juga: Soal UN Trigonometri dan Soal SBMPTN berkaitan Trigonometri