SOAL DAN PEMBAHASAN DIMENSI TIGA

Sebelumnya kita bahas tentang rumus penting pada dimensi tiga, sekarang adalah contoh soal dari materi tersebut.

Soal 1. Jarak titik ke titik

Pada kubus $ABCD.EFGH$ dengan rusuk $6\ cm$, titik $P$ di tengah rusuk $AB$. Tentukan jarak titik $P$ ke $G$.

Pembahasan

Perhatikan gambar di bawah ini!

Dari gambar di atas, titik $P$ dan $G$ terletak pada $\Delta PCG$ dan siku-siku di titik $C$. Jadi dengan menggunakan Phytagoras dapat ditentukan panjang $PG$. Terlebih dahulu kita cari panjang $PC$. $PC=\sqrt{PB^2+BC^2}=\sqrt{3^2+6^2}=\sqrt{45}=3\sqrt{5}$.

⧭$PG=\sqrt{PC^2+CG^2}$

        $=\sqrt{(3\sqrt{5})^2+6^2}$

        $=\sqrt{45+36}$

        $=\sqrt{81}=9\ cm$

Soal 2. Jarak titik ke garis

Pada kubus $ABCD.EFGH$ dengan rusuk $4\ cm$, tentukan jarak titik $A$ ke garis $HB$!

Pembahasan

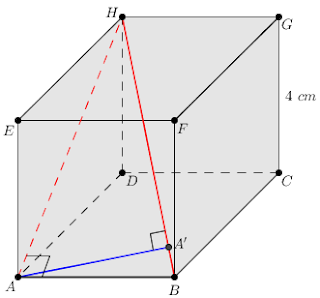
Perhatikan gambar di bawah ini!

Dari gambar di atas, jarak titik $A$ ke garis $HB$ adalah panjang $AA'$. Terlebih dahulu kita mencari panjang garis $AH$ [Diagonal Bidang] dan garis $HB$ [Diagonal Ruang] .  $AH=s\sqrt{2}=4\sqrt{2}$ dan $HB=s\sqrt{3}=4\sqrt{3}$

Perhatikan $\Delta ABH$! 

⧭$L_{ABH}=L_{ABH}$

⟺$\frac{1}{2}(AB)(AH)=\frac{1}{2}(HB)(AA')$

⟺$(4)(4\sqrt{2})=(4\sqrt{3})(AA')$

⟺$AA'=\frac{4}{3}{\sqrt{6}}\ cm$

Soal 3. Jarak titik ke bidang

Pada kubus $ABCD.EFGH$ dengan rusuk $12\ cm$, tentukan jarak titik $A$ ke bidang $HDF$

Pembahasan

Perhatikan gambar di bawah ini!

Dari gambar di atas, jarak titik $A$ ke bidang $HDF$ adalah jarak titik $A$ ke bidang $HDBF$ [Karena bidang bisa diperluas]. Untuk mencari jarak tersebut, kita akan membuat bidang yang melalui titik $A$ dan tegak lurus dengan bidang $HDBF$. Bidang yang tegak lurus tersebut adalah bidang $ACGE$. Perpotongan antara bidang $HDBF$ dengan bidang $ACGE$ adalah garis $XY$. Jadi jarak titik $A$ ke bidang $HDF$ adalah jarak titik $A$ dengan garis $XY$.
⧭ Perhatikan $\Delta AYX$, karena siku-siku di $Y$ maka jarak titik $A$ dengan garis $XY$ adalah panjang garis $AY$ yaitu setengah dari diagonal bidang $AC=\frac{1}{2}.12\sqrt{3}=6\sqrt{3}\ cm$

Lihat kembali: Rumus penting pada dimensi tiga

RUMUS PENTING PADA DIMENSI TIGA

Dimensi tiga merupakan materi yang diajarkan di SMA kelas 3 pada kurikulum 2013. Pada pembahasan kali ini, saya hanya menyinggung sedikit tentang materi ini yaitu pada pembahasan mencari jarak antara dua titik, jarak antara titik dengan garis, jarak antara titik dengan bidang.

1) Jarak antara titik dengan titik

Untuk mencari jarak antara titik dengan titik sering kali digunakan Rumus Phytagoras. Rumus Phytagoras ini dapat digunakan pada segitiga siku-siku.

Pada segitiga di samping, terlihat bahwa segitiga tersebut siku-siku di titik $B$. Oleh karena itu dapat dibuat persamaan Phytagorasnya adalah $(AC)^2=(AB)^2+(BC)^2$ atau 

$b^2=c^2+a^2$ atau

$c^2=b^2-a^2$ atau

$a^2=b^2-c^2$

Trik: 

1. Gambarkan titik yang dimaksud [Biasanya soal pada kubus atau balok]

2. Buat segitiga siku-siku yang melalui titik tersebut.

3. Cari jarak titik ke titik menggunakan Rumus Phytagoras.

2) Jarak antara titik dengan garis

Jarak titik $P$ ke garis $g$ adalah ruas garis terpendek yang menghubungkan titik $p$ ke garis $g$. Ruas garis terpendek tersebut diperoleh dengan menarik garis dari titik $P$ tegak lurus terhadap garis $g$. 

Perhatikan gambar di bawah!

Jarak titik $P$ ke garis $g$ adalah jarak titik $P$ ke titik $P'$.

⧭Untuk mencari jarak antara titik dengan garis, ada beberapa hal penting yang harus dipahami.

a. Rumus Phytagoras [seperti yang sudah dijelaskan di atas]
b. Rumus Luas Segitiga

Terdapat tiga rumus untuk mencari luas segitiga, tergantung yang mana yang dibutuhkan.

➤ Jika sebuah segitiga diketahui panjang alas dan tingginya, untuk mencari luas segitiga dapat dilihat gambar di bawah.

Luas segitiga adalah $\frac{1}{2}alas\times tinggi$

Luas segitiga $ABC$ di samping adalah

$L_{\Delta ABC}=\frac{1}{2}BC\times AB$

$L_{\Delta ABC}=\frac{1}{2}AC\times BD$

[Ingat: Tinggi segitiga merupakan tegak lurus dengan alasnya]

$L_{\Delta ABC}=L_{\Delta ABC}$

$\frac{1}{2}BC\times AB=\frac{1}{2}AC\times BD$

$BC\times AB=AC\times BD$

➤ Jika sebuah segitiga diketahui dua sisinya dan sudut yang diapit oleh sisi-sisi tersebut.

Luas segitiga $ABC$ di samping adalah
$L_{\Delta ABC}=\frac{1}{2}BC\times AB \times sin\ {\beta }$
$L_{\Delta ABC}=\frac{1}{2}BC\times AC \times sin\ {\gamma }$
$L_{\Delta ABC}=\frac{1}{2}AC\times AB \times sin\ {\alpha }$

➤ Jika sebuah segitiga diketahui ketiga sisinya, luas segitiga dapat dicari

$L_{\Delta ABC}=\sqrt{s(s-a)(s-b)(s-c)}$ dengan $s=\frac{a+b+c}{2}$

c. Rumus trigonometri aturan sin, cos, dan tan

Berdasarkan gambar di samping, bahwa
$sin\ {\alpha }=\frac{depan}{miring}=\frac{AC}{AB}$
$cos\ {\alpha }=\frac{samping}{miring}=\frac{BC}{AB}$
$tan\ {\alpha }=\frac{depan}{samping}=\frac{AC}{BC}$








d. Aturan cosinus
Aturan cosinus digunakan untuk mencari salah satu sudut jika diketahui ketiga sisi-sisinya atau untuk mencari salah satu sisi jika diketahui panjang sisi-sisi lainnya dan sudut yang diapit oleh sisi-sisi tersebut.

Berdasarkan gambar di samping, bahwa
$a^2=b^2+c^2-2bc.cos\ (A)$
$b^2=a^2+c^2-2ac.cos\ (B)$
$c^2=a^2+b^2-2ab.cos\ (C)$

Trik:

1. Gambarkan titik dan garis yang dimaksud [Biasanya soal pada kubus atau balok]

2. Buat segitiga yang melalui titik dan garis tersebut [Usahakan buat segitiga yang siku-siku]

3. Cari jarak titik ke garis yaitu panjang garis dari titik tersebut yang tegak lurus dengan garis [seringnya menggunakan luas segitiga]

3. Jarak antara titik dengan bidang

Jarak titik $P$ ke bidang $v$ adalah ruas garis terpendek yang menghubungkan titik $P$ ke bidang $v$. Ruas garis terpendek tersebut diperoleh dengan menarik garis dari titik $P$ tegak lurus dengan bidang $v$

Perhatikan gambar di bawah.

$PP'=$ merupakan jarak titik $P$ ke bidang $v$

Trik: Ubahlah jarak titik $P$ ke bidang $v$ menjadi jarak titik $P$ ke garis $g$
1. Lukislah bidang $w$ yang melalui $P$ dan tegak lurus $v$
2. Lukis garis $g$ yang merupakan perpotongan antara bidang $v$ dan $w$.
3. Jarak titik $P$ ke bidang $v$ adalah jarak titik $P$ ke garis $g$ [Kemudian selesaikan dengan trik mencari jarak titik ke garis seperti penjelasan sebelumnya].

Lihat: Soal dan pembahasan mengenai jarak titik ke titik, titik ke garis, dan titik ke bidang

Distribusi Normal

Distribusi Normal merupakan distribusi dengan variabel acak kontinu. Distribusi Normal juga sering disebut dengan Distribusi Gauss. Ada beberapa sifat penting dari distribusi normal, yaitu:

1. Grafik simetri terhadap garis tegak $x=\mu$, dengan $\mu$ adalah rata-rata.

2. Grafik selalu berada di atas sumbu $X$ atau $f(x)>0$

3. Mempunyai satu nilai modus

4. Grafiknya mendekati sumbu $X$ tetapi tidak pernah memotong sumbu $X$ [Sumbu $x$ merupakan asimtot datar]

5. Luas daerah di bawah kurva $f(x)$ dan di atas sumbu $X$ sama dengan 1, yaitu $P(-\infty<x<\infty)=1$

Persamaan umum distribusi normal adalah $f(x)=\frac{1}{\sigma \sqrt{2\pi }}e ^{-\frac{1}{2}\left ( \frac{x-\mu}{\sigma } \right )^{2}}$

MENENTUKAN PELUANG DISTRIBUSI NORMAL

Peluang distribusi normal $f(x)$ pada interval $a<x<b$ ditentukan dengan menghitung luas daerah di bawah kurva $f(x)$ dan di atas sumbu $X$. Kalau disajikan dalam gambar akan tampak seperti di bawah ini.

Berdasarkan gambar di atas, luas daerah di bawah grafik dan di atas sumbu x adalah 1 dan garis tegak $x=\mu$ merupakan garis sumbu simetri oleh karena itu di sebelah kanan garis $x=\mu$ mempunyai luas $\frac{1}{2}$. Begitupun untuk luas di sebelah kiri $x=\mu$. 

Luas daerah di atas adalah $P(a<x<b)=\int_{a}^{b}{\frac{1}{\sigma \sqrt{2\pi }}e ^{-\frac{1}{2}\left ( \frac{x-\mu}{\sigma } \right )^{2}}}dx$. Proses pengintegralan tersebut sulit untuk dilakukan, oleh karena itu penyelesaianya dilakukan dengan menggunakan transformasi nilai-nilai $X$ menjadi nilai-nilai baku $Z$ yaitu $Z=\frac{x-\mu }{\sigma }$.  Dengan tranformasi tersebut, diperoleh rata-rata $\mu=0$ dan $\sigma=1$, sehingga distribusi $f(x)$ berubah menjadi $f(Z)$ dengan persamaan $f(Z)=\frac{1}{\sqrt{2\pi }}e^{^-\frac{1}{2}Z^{2}},-\infty <Z<\infty$.

Jadi peluang $P(z_1<Z<z_2)=\int_{z_1}^{z_2}\frac{1}{\sqrt{2\pi }}e^{^-\frac{1}{2}Z^{2}}dx$

Dengan nilai  $P(z_1<Z<z_2)$ dapat dihitung menggunakan table Z.

Distribusi peubah acak normal dengan rataan $0$ dan simpangan baku $1$ disebut dengan distribusi normal baku.

CONTOH SOAL

([1]) Diketahui suatu variable acak $X$ mempunyai distribusi normal dengan rata-rata $18$ dan simpangan baku $\frac{5}{2}$. Nilai dari $P(17<X<21)$ adalah …

Jawab.

Diketahui di soal bahwa $\mu=18$ dan $\sigma =\frac{5}{2}$ dan dapat dicari $z_1=\frac{x_1-\mu}{\sigma}=\frac{17-18}{\frac{5}{2}}=-0,4$ dan $z_2=\frac{x_2-\mu}{\sigma}=\frac{21-18}{\frac{5}{2}}=1,2$.

Maka nilai $P(17<X<21)$ ditranformasikan menjadi $P(-0,4<Z<1,2)$

$P(-0,4<Z<1,2)=P(0<Z<0,4)+P(0<Z<1,2)=0,1554+0,3849=0,5303$. 

Catatan: luas daerah kurva normal antara dengan $-0,4<Z<0=0<Z<0,4$

([2]) Suatu variabel acak (X) memenuhi distribusi normal baku . Nilai $P(1,42<Z<2,54)$ adalah

Jawab. 

$P(1,42<Z<2,54)=P(0<Z<2,54)-P(0<Z<1,42)=0,4945-0,4222=0,0723$

Cara membaca table Z
Misalkan kita akan menentukan nilai dari $P(0<Z<1,42)$. Yang perlu diperhatikan adalah angka 1,42 yang kita pecah menjadi 1,4 dan 2. Angka 1,4 kita lihat pada table sebelah kiri secara vertical dan angka 2 lihat di atas table secara horizontal. Hubungkan kedua angka tersebut seperti menghubungkan titik pada koodinat kartesius. Dalam table akan ketemu $P(0<Z<1,42)=0,4222$. Untuk lebih jelasnya dapat dilihat pada gambar di bawah.

 Dalam kurva normal akan tampak seperti di bawah ini.

Berkas Lingkaran

Berkas Lingkaran merupakan lingkaran-lingkaran yang dapat dibuat dari titik potong dua lingkaran. Kalau kedua lingkaran itu $L_1=0$ dan $L_2=0$, maka berkas lingkaran itu $L_1+\lambda\ L_2=0$ dimana $L_1$ dan $L_2$ disebut dengan lingkaran dasar dan kedua titik potongnya disebut dengan titik-titik dasar.

Pada pembahasan kali ini, terdapat dua kasus dalam berkas lingkaran.
❤Kasus Pertama: Kedua lingkaran saling berpotongan
Untuk lebih jelasnya dapat dilihat pada gambar di bawah ini.

Pada gambar di atas terlihat bahwa lingkaran dasarnya adalah $L_1$ dan $L_2$ yang berwarna merah dan berpotongan di dua titik yaitu titik $A$ dan $B$.
❤Kasus Kedua: Kedua lingkaran saling bersinggungan
Untuk lebih jelasnya dapat dilihat pada gambar di bawah ini.

Pada gambar di atas terlihat bahwa lingkaran dasarnya adalah $L_1$ dan $L_2$ yang berwarna merah saling bersinggungan. Titik $A$ merupakan titik singgung kedua lingkaran.

     Sifat istimewa yang dimiliki anggota berkas lingkaran adalah bahwa semua anggota berkas lingkaran mempunyai sebuah garis kuasa dan pusatnya berada pada garis lurus yang menghubungkan kedua titik pusat lingkaran dasarnya [sentral].

Berikut merupakan contoh soal dari berkas lingkaran
Soal 1. Tentukan persamaan lingkaran yang melalui $O$ dan titik potong kedua lingkaran $x^2+y^2-6x-8y-11=0$ dan $x^2+y^2-4x-6y-22=0$.
Pembahasan
      $L_1\equiv x^2+y^2-6x-8y-11=0$
      $L_2\equiv x^2+y^2-4x-6y-22=0$
Persamaan lingkaran yang ditanyakan akan berbentuk
      $L_1+\lambda L_2=0$
      $x^2+y^2-6x-8y-11+\lambda (x^2+y^2-4x-6y-22)=0$
Karena lingkaran yang ditanyakan melalui $O$, maka substitusi $(0,0)$ ke $x^2+y^2-6x-8y-11+\lambda (x^2+y^2-4x-6y-22)=0$
      $0^2+0^2-6.0-8.0-11+\lambda (0^2+0^2-4.0-6.0-22)=0$
      $-22\lambda=11$
      $\lambda=-\frac{1}{2}$
Jadi, persamaan lingkaran yang dicari adalah
$x^2+y^2-6x-8y-11+\lambda (x^2+y^2-4x-6y-22)=0$
$x^2+y^2-6x-8y-11-\frac{1}{2}(x^2+y^2-4x-6y-22)=0$
$2x^2+2y^2-12x-16y-22-x^2-y^2+4x+6y+22=0$
$x^2+y^2-8x-10y=0$
Soal 2. Tentukan persamaan lingkaran yang melalui perpotongan lingkaran $x^2+y^2-x+7y-3=0$ dan $x^2+y^2-5x-y+1=0$ yang berpusat di garis $x-y=0$
Pembahasan
    $L_1\equiv x^2+y^2-x+7y-3=0$
    $L_2\equiv x^2+y^2-5x-y+1=0$
Berdasarkan sifat istimewa dari berkas lingkaran bahwa pusat dari berkas lingkaran berada pada garis yang menghubungkan kedua pusat dari lingkaran dasar. Berdasarkan persamaan lingkaran di atas, pusat lingkaran 1[$P_1(\frac{1}{2},-\frac{7}{2})$] dan lingkaran 2 [$P_2(\frac{5}{2},\frac{1}{2})$]. Maka persamaan garis yang menghubungkan kedua persamaan lingkaran tersebut adalah
    $\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$
    $\frac{y+\frac{7}{2}}{\frac{1}{2}-\frac{7}{2}}=\frac{x-\frac{1}{2}}{\frac{5}{2}-\frac{1}{2}}$
    $\frac{y+\frac{7}{2}}{4}=\frac{x-\frac{1}{2}}{2}$
    $2y+7=4x-2$
    $4x-2y=9$
Karena titik pusat lingkaran yang kita cari berada pada garis $4x-2y=9$ dan $x-y=0$. Maka titik pusat lingkaran yang kita cari berada pada perpotongan garis $4x-2y=9$ dan $x-y=0$. $x$ dan $y$ kita cari menggunakan cara substitusi atau eliminasi dari kedua persamaan tersebut, dan di dapat hasilnya $x=\frac{9}{2}$ dan $y=\frac{9}{2}$. Maka titik pusatnya $\left ( \frac{9}{2},\frac{9}{2} \right )$.
Persamaan lingkaran yang di cari akan berbentuk $L_1+\lambda L_2=0$
    $x^2+y^2-x+7y-3+\lambda (x^2+y^2-5x-y+1)=0$
    $(1+\lambda )x^2+(1+\lambda )y^2-(1+5\lambda)x+(7-\lambda)y-3+\lambda=0$
    $x^2+y^2-\left ( \frac{1+5\lambda}{1+\lambda} \right )x+\left ( \frac{7-\lambda}{1+\lambda}\right )y+\frac{3+\lambda}{1+\lambda}=0$
Berdasarkan persamaan lingkaran di atas, maka absis [sumbu-x] dari pusat lingkaran tersebut adalah
    $-\frac{1}{2}\left ( -\left ( \frac{1+5\lambda}{1+\lambda} \right ) \right )=\frac{9}{2}$
    $\frac{1+5\lambda}{1+\lambda}=9$
    $1+5\lambda=9+9\lambda$
    $\lambda=-2$
Ordinat dari pusat lingkaran juga bisa di gunakan, dan tetap di dapat $\lambda=-2$
Jadi persamaan lingkarannya adalah
    $x^2+y^2-x+7y-3+\lambda (x^2+y^2-5x-y+1)=0$
    $x^2+y^2-x+7y-3-2(x^2+y^2-5x-y+1)=0$
    $x^2+y^2-x+7y-3-2x^2+-2y^2+10x+2y-2=0$
    $x^2+y^2-9x-9y+5=0$

Soal Kuasa, Titik Kuasa dan Garis Kuasa

Soal 1. Berapakah kuasa $(3,2)$ terhadap lingkaran $x^2+y^2+2x-6y+1=0$? Apakah titik tersebut di dalam atau di luar lingkaran?

Penyelesaian
Kuasa titik $(3,2)=(x_1,y_1)$ terhadap lingkaran $x^2+y^2+2x-6y+1=0$ adalah $(x_1)^2+(y_1)^2+2x_1-6y_1+12$
$=(3)^2+(2)^2+2.3-6.2+1$
$=9+4+6-12+1=8$
❤Jadi kuasanya $8$

Soal 2. Tentukan garis kuasa kedua lingkaran $x^2+y^2=25$ dan $x^2+y^2-6x-8y-11=0$.

Penyelesaian
$L_1\equiv x^2+y^2-25=0$
$L_2\equiv x^2+y^2-6x-8y-11=0$
Garis kuasa kedua lingkaran tersebut akan berbentuk $L_1-L_2=0$
$x^2+y^2-25=0-\left ( x^2+y^2-6x-8y-11=0 \right )$
$6x+8y+11-25=0$
$3x+4y-7=0$
❤Jadi garis kuasanya adalah $3x+4y-7=0$

Soal 3. Tentukan sebuah titik yang mempunyai kuasa yang sama terhadap ketiga lingkaran $(x-1)^2+(y+2)^2=3$, $x^2+(y-2)^2=5$ dan $(x+5)^2+y^2=16$.

Penyelesaian
$L_1\equiv\ (x-1)^2+(y+2)^2-3=0$
         $x^2-2x+1+y^2+4y+4-3=0$
         $x^2+y^2-2x+4y+2=0$
$L_2\equiv\ x^2+(y-2)^2=5$
         $x^2+y^2-4y+4-5=0$
         $x^2+y^2-4y-1=0$
$L_3\equiv\ (x+5)^2+y^2=16$
         $x^2+10x+25+y^2-16=0$
         $x^2+y^2+10x+9=0$
Berdasarkan tiga persamaan lingkaran, dapat dibuat tiga  persamaan garis kuasa. Tetapi untuk mencari titik kuasa cukup diperlukan dua persamaan garis kuasa.
$g_1\equiv L_1-L_2=0$
         $x^2+y^2-2x+4y+2-(x^2+y^2-4y-1)=0$
         $-2x+8y+3=0$ .................... $(a)$
$g_1\equiv L_2-L_3=0$
         $x^2+y^2-4y-1-(x^2+y^2+10x+9)=0$
         $-10x-4y-10=0$ .................. $(b)$
❤Berdasarkan persamaan $(a)$ dan $(b)$, dengan menggunakan metode eliminasi atau substitusi di dapat $x=-\frac{17}{22}$ dan  $y=-\frac{25}{44}$

Klik untuk melihat materi kuasa, titik kuasa dan garis kuasa

Apa Itu Kuasa, Garis Kuasa dan Titik Kuasa

☺☺☺Kuasa Titik Terhadap Satu Lingkaran☺☺☺
Perhatikan gambar di bawah ini.

Berdasarkan gambar di atas, terdapat banyak sekali garis yang dapat ditarik dari titik (P) ke lingkaran dengan pusat (L). Beberapa garis tersebut adalah garis $c,d,e,f,g$. Dapat di lihat di gambar bahwa $PA.PA'=PB.PB'=PC.PC'=(PR)^2=(PQ)^2=(PL)^2-r^2$ [Pembuktian bisa menggunakan kesebangunan]. Hasil kali yang tetap tersebut merupakan kuasa titik (P) terhadap lingkaran (L). Kuasa titik (P) terhadap lingkaran (L) kita sebut (K_P). Jadi $K_P=(PL)^2-r^2$.

❤Kuasa titik $P(x_1,y_1)$ terhadap $L\equiv (x)^2+(y)^2=r^2$ adalah $K_P=(x_1)^2+(y_1)^2-r^2$.

❤Kuasa titik $P(x_1,y_1)$ terhadap $L\equiv (x-a)^2+(y-b)^2=r^2$ adalah $K_P=(x_1-a)^2+(y_1-b)^2-r^2$.

❤Kuasa titik $P(x_1,y_1)$ terhadap $L\equiv x^2+y^2+Ax+By+C$ adalah $K_P=(x_1)^2+(y_1)^2+Ax_1+By_1+C$.

Jadi kesimpulan kuasa titik terhadap lingkaran adalah:

1. $K_P>0$, maka titik (P) berada di luar lingkaran

2. $K_P=0$, maka titik (P) berada pada lingkaran

3. $K_P<0$, maka titik (P) berada di dalam lingkaran

☺☺☺Kuasa Titik Terhadap Dua Lingkaran☺☺☺

Perhatikan gambar di bawah!

Garis hubung antara (L_1) dan (L_2) di sebut sentral. Misalkan titik (P) mempunyai kuasa yang sama terhadap (L_1) dan (L_2). Maka:

Kuasa titik $P(x_1,y_1)$ terhadap $L_1$ adalah $K_PL_1=(x_1)^2+(y_1)^2+Ax_1+By_1+C$
Kuasa titik $P(x_1,y_1)$ terhadap $L_2$ adalah $K_PL_2=(x_1)^2+(y_1)^2+Qx_1+Ry_1+S$
Karena mempunyai kuasa yang sama, maka $K_PL_1=K_PL_2$
$(x_1)^2+(y_1)^2+Ax_1+By_1+C=$
$(x_1)^2+(y_1)^2+Qx_1+Ry_1+S$
$(A-Q)x_1+(B-R)y_1+(C-S)=0$
Bentuk di atas adalah linier, maka grafiknya berupa garis lurus yang di sebut dengan garis kuasa dua lingkaran.

❤ Misalkan terdapat dua lingkaran  (L_1) dan (L_2), Garis Kuasa kedua lingkaran tersebut adalah $L_1-L_2=0$ atau $L_2-L_1=0$. 

Garis kuasa tegak lurus dengan sentral.

❤ Tempat kedudukan titik-titik yang mempunyai kuasa yang sama terhadap dua buah lingkaran merupakan sebuah garis kuasa yang tegak lurus dengan sentral.

☺☺☺Kuasa Titik Terhadap Tiga Lingkaran☺☺☺
Perhatikan gambar di bawah ini!

❤Tiga buah lingkaran hanya mempunyai sebuah titik kuasa yakni titik yang mempunyai kuasa yang sama terhadap tiga lingkaran.

Langkah mencari titik kuasa:

Cari garis $g_1,\ g_2,\ g_3$ dengan ketentuan $g_1\equiv L_1-L_2=0$, $g_2\equiv L_2-L_3=0$, $g_3\equiv L_3-L_1=0$. Mencari titik kuasa cukup diperlukan dua garis kuasa dari tiga garis kuasa yang di dapat dengan cara eliminasi, substitusi, maupun metode lainnya untuk mencari titik potong kedua garis. Garis yang digunakan yaitu $g_1\ dan \  g_2$ atau $g_1\ dan\  g_3$ atau $g_2\ dan\  g_3$. Dari ketiga pilihan tersebut akan mendapatkan hasil yang sama.

Klik untuk melihat soal mengenai kuasa, garis kuasa dan titik kuasa

Menentukan Titik Belok dari Turunan Pertama dan Turunan Kedua

Penggunaan turunan untuk menggambar grafik adalah untuk menentukan titik stasioner dan titik belok. Namun pada pembahasan sekarang akan di bahas titik belok. Sebelum kita menentukan cara titik belok, terlebih dahulu kita pengaruh turunan pertama dan kedua terhadap grafik.

$\bigstar$ Turunan Pertama

Misalkan (f) kontinu pada interval (I) dan terdeferensialkan pada setiap titik-dalam dari (I).

1. Jika $f'(x)>0$ untuk semua titik-dalam (I), maka (f) naik pada (I)

2. Jika $f'(x)<0$ untuk semua titik-dalam (I), maka (f) turun pada (I)

Untuk lebih jelasnya, perhatikan gambar di bawah ini.

Berdasarkan gambar di atas, garis $p$ merupakan garis singgung grafik. Perlu di ingat bahwa gradien garis singgung merupakan turunan dari grafik. Garis $p$ miring ke kanan maka mempunyai gradien positif [$f'(x)>0$]. Sedangkan Garis $t$ miring ke kiri maka mempunyai gradien negatif [$f'(x)<0$]

Dapat dilihat bahwa, pada rentang yang mempunyai garis singgung bergradien positif grafik naik, sendangkan pada rentang yang mempunyai garis singgung bergradien negatif grafik turun

$\bigstar$ Turunan Kedua

Misalkan (f) kontinu pada interval (I) dan terdeferensialkan pada setiap titik-dalam dari (I)

1. Jika $f''(x)>0$ untuk semua titik-dalam (I), maka $f(x)$ cekung ke atas

2. Jika $f''(x)<0$ untuk semua titik-dalam (I), maka $f(x)$ cekung ke atas

Selain untuk melihat kecekungan dari grafik, kegunaan turunan kedua adalah untuk menentukan titik belok dari suatu grafik. 

Menentukan titik belok.

Misalkan $f(x)$ adalah fungsi yang terdeferensialkan dua kali pada $x=p$, dan $(f''(p)=0)$.

1. Titik $(p,f(p))$ merupakan titik belok jika $f''(x)<0$ untuk (x<a) fungsi (f(x)) cekung ke bawah dan $f''(x)>0$ untuk (x>a) fungsi (f(x)) cekung ke atas

2. Titik $(p,f(p))$ merupakan titik belok jika $f''(x)>0$ untuk (x<a) fungsi (f(x)) cekung ke atas dan $f''(x)<0$ untuk (x>a) fungsi (f(x)) cekung ke bawah.

Untuk lebih jelasnya, perhatikan gambar di bawah ini.

Berdasarkan gambar di samping, titik merupakan titik belok, karena di sebelah kiri titik D kurva cekung ke bawah dan di sebelah kanan titik D kurva cekung ke atas. Atau sebaliknya, Titik belok terjadi saat di sebelah kiri titik tersebut kurva cekung ke atas dan di sebelah kanan titik tersebut kurva cekung ke bawah.

Titik D di sebut titik belok juga bisa kita uji menggunakan turunan pertama. Perhatikan gambar di bawah ini.

Dari gambar di atas, terlihat bahwa titik D adalah titik belok karena di sebelah kiri dan kanan titik D adalah fungsi naik. Titik belok juga terjadi saat di sebelah kiri dan kanan titik tersebut adalah fungsi turun.
Untuk lebih jelasnya bisa lihat contoh berikut.
Soal 1. Tentukan titik belok dan titik stasioner dari fungsi berikut.
$y=x^4-2x^3$
Jawab.

$y=f(x)=x^4-2x^3$
$y'=f'(x)=4x^3-6x^2$
$0=4x^3-6x^2$
$0=2x^3-3x^2$
$0=x^2(2x-3)$
$x=0\ atau\ x=\frac{3}{2}$
Untuk uji tanda turunan pertama perhatikan gambar di bawah!

Dari Uji titik tersebut dapat dilihat bahwa titik stasioner terjadi saat $x=0$ dan $x=\frac{3}{2}$. Pada saat $x=0$ sekaligus sebagai titik belok karena di sebelah kiri maupun kanan titik tersebut disebut sebagai fungsi turun.

Dari turunan pertama di atas, di dapat turunan keduanya
$y''=f''(x)=12x^2-12x$
$0=12x^2-12x$
$0=12x(x-1)$
$x=0\ atau\ x=1$
Untuk uji tanda turunan kedua perhatikan gambar di bawah!

Dari uji titik tersebut, terlihat bahwa titik belok ada pada saat $x=0$ dan $x=1$ karena di sebelah kiri maupun kanan titik tersebut berbeda arah kecekungannya.
Berikut adalah gambar dari grafik di atas.

Soal Masuk Perguruan Tinggi Materi Trigonometri

Soal UMB 2015
Jika $\Theta$ adalah sudut di kuadran 4 yang memenuhi $tan^2\ \Theta =4sin^2\ \Theta$, maka $sin\ \Theta +cos\ \Theta = ...$
A. $1-\sqrt{3}$
B. $\frac{1}{2}(1-\sqrt{3})$
C. $-\frac{1}{2}(1-\sqrt{3})$
D. $-(1-\sqrt{3})$
E. $2-\sqrt{3}$

Pembahasan
$\bigstar\ tan^2\ \Theta =4sin^2\ \Theta$
$\frac{sin^2\ \Theta}{cos^2\ \Theta } =4sin^2\ \Theta$
$\frac{1}{cos^2\ \Theta } =4,\ karena\ sin^2\ \Theta\neq 0$
$cos^2\ \Theta =\frac{1}{4}$
$cos\ \Theta =\pm \sqrt{\frac{1}{4}}$
$cos\ \Theta =\pm \frac{1}{2}$
$\bigstar\ Ambil\ cos\ \Theta =\frac{1}{2},\ karena\ \Theta\ di\ kuadran\ 4$
Untuk mencari $cos\ \Theta$ gunakan Pytagoras, dan hasilnya akan seperti berikut.

dari gambar di samping, di dapat $sin\ \Theta =-\frac{\sqrt{3}}{2}$, tanda negatif karena berada nilai (sinus) di kuadran 4 adalah negatif. Jadi $sin\ \Theta +cos\ \Theta =-\frac{\sqrt{3}}{2}+\frac{1}{2}=\frac{1}{2}(1-\sqrt{3})$
Jawaban B

Soal UMB 2016
Pada gambar $\Delta ABC$ berikut. $\frac{cos\ \alpha }{a}+\frac{cos\ \beta }{b}+\frac{cos\ \gamma }{c}=$

A. $\frac{a+b+c}{abc}$
B. $\frac{a+b+c}{2abc}$
C. $\frac{2(a+b+c)}{abc}$
D. $\frac{a^2+b^2+c^2}{abc}$
E. $\frac{a^2+b^2+c^2}{2abc}$

Catatan Untuk Pembahasan
Untuk menjawab soal ini, kita gunakan aturan (cosinus). Berdasarkan gambar di atas, maka aturan (cosinus)-nya
$a^2=b^2+c^2-2bc.cos\ \alpha \Leftrightarrow cos\ \alpha =\frac{b^2+c^2-a^2}{2bc}$
$b^2=a^2+c^2-2ac.cos\ \beta \Leftrightarrow cos\ \beta =\frac{a^2+c^2-b^2}{2ac}$
$c^2=a^2+b^2-2ab.cos\ \gamma \Leftrightarrow cos\ \gamma =\frac{a^2+b^2-c^2}{2ab}$

Pembahasan
$\bigstar\ \frac{cos\ \alpha }{a}+\frac{cos\ \beta }{b}+\frac{cos\ \gamma }{c}$
$=\frac{\frac{b^2+c^2-a^2}{2bc}}{a}+\frac{\frac{a^2+c^2-b^2}{2ac}}{b}+\frac{\frac{a^2+b^2-c^2}{2ab}}{c}$
$=\frac{b^2+c^2-a^2}{2abc}+\frac{a^2+c^2-b^2}{2abc}+\frac{a^2+b^2-c^2}{2abc}$
$=\frac{b^2+c^2-a^2+a^2+c^2-b^2+a^2+b^2-c^2}{2abc}$
$=\frac{a^2+b^2+c^2}{2abc}$
Jawaban E

Rumus dan Teorema Penting dalam Integral

Setelah kita memahami perbedaan integral tentu dan tak tentu. Berikut merupakan rumus-rumus dan beberapa teorema yang penting dalam integral:

1. [Teorema]: Jika $f$ periodik dengan periode (p), maka $\int_{a+p}^{b+p}f(x)dx=\int_{a}^{b}f(x)dx$
2. [Teorema Nilai Rata-rata untuk Integral]: Jika (f) kontinu pada $[a,b]$, maka terdapat suatu bilangan (c) antara (a) dan (b) sedemikian sehingga $\int_{a}^{b}f(t)dt=f(c)(b-a)$
3. [Teorema pendeferensialan suatu Integral Tentu]: Andaikan (f) kontinu pada selang tertutup $[a,b]$ dan andaikan (x) sebuah $(variabel)$ titik dalam $[a,b]$. Maka $D_x\left [ \int_{a}^{x}f(t)dt \right ]=f(x)$
   $D_x$ merupakan turunan terhadap (x)
4. [Teorema Keterbatasan]: Jika (f) terintegralkan pada $[a,b]$ dan jika $m\leq f(x)\leq M$ untuk semua (x) dalam $[a,b]$, maka $m(b-a)\leq \int_{a}^{b}f(x)dx\leq M(b-a)$
5. [Teorema Perbandingan]: Jika (f) dan (g) terintegralkan pada $[a,b]$ dan jika $f(x)\leq g(x)$ untuk semua (x) dalam $[a,b]$, maka $\int_{a}^{b}f(x)dx\leq \int_{a}^{b}g(x)dx$

$\bigstar$ Bentuk-Bentuk Dasar Integral

1. $\int x^{-1}dx=ln|x|+c$
2. $\int e^x\ dx=e^x+C$
3. $\int a^x\ dx=\frac{a^x}{ln\ a}+C$
4. $\int \frac{du}{\sqrt{a^2-u^2}}=sin^{-1}\frac{u}{a}+C$
5. $\int \frac{du}{a^2+u^2}=\frac{1}{a}tan^{-1}\ \frac{u}{a}+C$
6. $\int \frac{du}{a^2-u^2}=\frac{1}{2a}ln\left | \frac{u+a}{u-a} \right |+C$
7. $\int \frac{du}{u\sqrt{u^2-a^2}}=\frac{1}{a}sec^{-1}\left | \frac{u}{a} \right |+C$

$\bigstar$ Integral Trigonometri

1. $\int cos\ (ax+b)dx=\frac{1}{a}sin\ (ax+b)+c$
2. $\int sin\ (ax+b)dx=-\frac{1}{a}cos\ (ax+b)+c$
3. $\int sec^2\ (ax+b)dx=\frac{1}{a}tan\ (ax+b)+c$
4. $\int csc^2\ (ax+b)dx=-\frac{1}{a}cot\ (ax+b)+c$
5. $\int sec\ (ax+b).tan\ (ax+b)dx=\frac{1}{a}sec\ (ax+b)+c$
6. $\int csc\ (ax+b).cot\ (ax+b)dx=-\frac{1}{a}csc\ (ax+b)+c$
7. $\int tan\ u\ dx=-ln|cos\ u|+C$
8. $\int cot\ u\ dx=ln|sin\ u|+C$
9. $\int sec\ u\ dx=ln|sec\ u+tan\ u|+C$
10. $\int csc\ u\ dx=ln|csc\ u-cot\ u|+C$

$\bigstar$ Bentuk-Bentuk Dasar Integral

1. $\int ue^u\ du=(u-1)e^u+C$
2. $\int ln\ u\ du=u\ ln\ u-u+C$
3. $\int u^ne^u\ du=u^ne^u-n\int u^{n-1}e^u\ du$
4. $\int u^n\ ln\ u\ du=\frac{u^{n+1}}{n+1}ln\ u-\frac{u^{n+1}}{(n+1)^2}+C$
5. $\int e^{au}sin\ bu\ du=\frac{e^{au}}{a^2+b^2}(a\ sin\ bu-b\ cos\ bu)+C$
6. $\int e^{au}cos\ bu\ du=\frac{e^{au}}{a^2+b^2}(a\ cos\ bu-b\ sin\ bu)+C$

Soal SBMPTN Integral

Soal SBMPTN 2017
Didefinisikan $f(x)$ fungsi ganjil $\leftrightarrow f(-x)=-f(x)$ dan $f(x)$ fungsi genap $\leftrightarrow f(-x)=f(x)$ untuk $x\epsilon\ riil$. Jika $\int_{-4}^{4}{f(x)(sin\ x+1)}dx=8$, dengan $f(x)$ fungsi genap dan $\int_{-2}^{4}{f(x)}dx=4$, maka $\int_{-2}^{0}{f(x)}dx=$ ...

Catatan untuk pembahasan:
Diketahui di soal bahwa $f(x)$ fungsi genap, maka $\int_{-4}^{4}f(x)dx=2\int_{0}^{4}f(x)dx$.
$sin\ x$ adalah fungsi ganjil $(sin\ (-x)=-sin\ (x))$, maka $f(x).sin\ x$ adalah fungsi ganjil, jadi $\int_{-4}^{4}(f(x).sin\ x)dx=0$.

Pembahasan
$\bigstar\ \int_{-4}^{4}{f(x)(sin\ x+1)}dx=8$
$\int_{-4}^{4}{\left ( f(x).sin\ x+f(x) \right )}dx=8$
$\int_{-4}^{4}{\left ( f(x).sin\ x \right )}dx+\int_{-4}^{4}f(x)dx=8$
$0+\int_{-4}^{4}f(x)dx=8$
$\int_{-4}^{4}f(x)dx=8$
$2\int_{0}^{4}f(x)dx=8$
$\int_{0}^{4}f(x)dx=4$
$\bigstar\ \int_{-2}^{4}f(x)dx=\int_{-2}^{0}f(x)dx+\int_{0}^{4}f(x)dx$
$4=\int_{-2}^{0}f(x)dx+4$
$\int_{-2}^{0}f(x)dx=0$

Soal Pola SBMPTN
Jika $\int_{-2}^{2}(x^3+3|x|+2x)dx=2p$, tentukan nilai p=...

Pembahasan:
Definisi harga mutlak $|x|=\left \{ \begin{matrix}x\ untuk\ x\geq 0\\-x\ untuk\ x<0\end{matrix} \right.$. Maka berdasarkan definisi tersebut,

$\int_{-2}^{2}(x^3+3|x|+2x)dx=2p$

$\int_{-2}^{0}(x^3+3(-x)+2x)dx+\int_{0}^{2}(x^3+3(x)+2x)dx=2p$
$\int_{-2}^{0}(x^3-x)dx+\int_{0}^{2}(x^3+5x)dx=2p$
$\left [ \frac{1}{4}x^4-\frac{1}{2}x^2 \right ]\begin{matrix}0\\ \\-2 \end{matrix}+\left [ \frac{1}{4}x^4-\frac{5}{2}x^2 \right ]\begin{matrix}2\\ \\0 \end{matrix}=2p$
$\left ( 0-\left ( \frac{1}{4}.16-\frac{1}{2}.4 \right ) \right )+\left ( \left ( \frac{1}{4}.16-\frac{5}{2}.4 \right )-0 \right )=2p$
$-(4-2)+4+10=2p$
$12=2p\Leftrightarrow p=6 $

Soal SBMPTN Trigonometri

Soal 1. SBMPTN 2017
Jika $x_1$ dan $x_2$ adalah solusi dari $\frac{2sin\ x.cos\ 2x}{cos\ x.sin\ 2x}-5tan\ x+5=0$, maka $tan\ (x_1+x_2)=...$
A. $-\frac{5}{7}$
B. $-\frac{5}{3}$
C. $\frac{\sqrt{5}}{7}$
D. $\frac{\sqrt{5}}{3}$
E. $\frac{5}{3}$

Pembahasan:
$\frac{2sin\ x.cos\ 2x}{cos\ x.sin\ 2x}-5tan\ x+5=0$
$\frac{2sin\ x.\left ( cos^2\ x-sin^2\ x \right )}{cos\ x.2sin\ x.cos\ x}-5tan\ x+5=0$
$\frac{2sin\ x.cos^2\ x}{2sin\ x.cos^2\ x}-\frac{2sin^3\ x}{2sin\ x.cos^2\ x}-5tan\ x+5=0$
$1-tan^2\ x-5tan\ x+5=0$
$-tan^2\ x-5tan\ x+6=0$
$tan^2\ x+5tan\ x-6=0$
Hasil di atas merupakan persamaan kuadrat dengan variabel $tan\ x$, dimana $a=1, b=5$, dan $c=-6$. Jadi:
$tan\ \left ( x_1+x_2 \right )=\frac{tan\ x_1+tan\ x_2}{1-tan\ x_1.tan\ x_2}$

$=\frac{-\frac{b}{a}}{1-\frac{c}{a}}$
$=\frac{-\frac{5}{1}}{1-\frac{-6}{1}}$
$=-\frac{5}{7}$

Jawaban A

Pembahasan Soal Masuk Perguruan Tinggi Materi Deret dan Barisan

Soal SIMAK UI 2015
Diketahui jumlah 50 suku pertama dari deret aritmatika adalah 200 dan jumlah 50 suku berikutnya adalah 2700. Suku pertama dari barisan tersebut adalah ...
A. -1221
B. -21,5
C. -20,5
D. 12
E. 8

Pembahasan
Berdasarkan soal di atas, dapat dituliskan dalam bahasa matematika seperti berikut.
$\therefore S_{50}=200\Leftrightarrow \frac{50}{2}(2a+(50-1)b)=200$

$2a+49b=8$
$b=\frac{8-2a}{49} ...... (1)$

$\therefore S_{100}=S_{50}+2700$
$S_{100}=2900\Leftrightarrow \frac{100}{2}(2a+(100-1)b)=2900$

$2a+99b=58 ....... (2)$

Berdasarkan persamaan $(1)$ dan $(2)$ di dapat:
$2a+99b=58$
$2a+99\left ( \frac{8-2a}{49} \right )=58$
$98a+792-198a=2842$
$-100a=2050$
$a=-20,5$
Jawaban C

Soal SBMPTN 2015
Jika $u_1,u_2,u_3, ...$ adalah barisan geometri yang memenuhi $u_3-u_6=x$ dan $u_2-u_4=y$, maka $x/y= ...$
A. $\frac{r^{3}-r^2-r}{r-1}$
B. $\frac{r^{3}-r^2+r}{r-1}$
C. $\frac{r^{3}+r^2+r}{r+1}$
D. $\frac{r^{3}+r^2-r}{r-1}$
E. $\frac{r^{3}-r^2+r}{r+1}$

Pembahasan
$\therefore u_3-u_6=x$
$ar^2-ar^5=x$
$a(r^2-r^5)=x$

$\therefore u_2-u_4=y$
$ar-ar^3=y$
$a(r-r^3)=y$

$\frac{x}{y}=\frac{a(r^2-r^5)}{a(r-r^3)}$
$=\frac{r^2(1-r^3)}{r(1-r^2)}$
$=\frac{r(1-r)(1+r+r^2)}{(1-r)(1+r)}$
$=\frac{1+r+r^2}{1+r}$
Jawaban C

Mencari Luas Daerah Menggunakan Integral

Seperti yang saya posting sebelumnya pada Perbedaan Integral Tentu dan Tak Tentu bahwa daerah yang dibentuk oleh grafik $y=f(x)$ adalah daerah yang tercakup di antara kurva $y=f(x)$ dan sumbu-(x).

• Jika daerah terletak di antara kurva $y=f(x)$ dan sumbu-(x) [berada di atas sumbu-(x)] dengan batas-batas integral (a) dan (b)
  
  
  Maka luas daerahnya adalah $\int_{a}^{b}{f(x)}\ dx$
• Jika daerah terletak di antara kurva $y=f(x)$ dan sumbu-(x) [berada di bawah sumbu-(x)] dengan batas-batas integral (a) dan (b)
  
  
  Maka luas daerahnya adalah $-\int_{a}^{b}{f(x)}\ dx$

Luas daerah tidak ada yang negatif.
Berikut merupakan contoh-contoh soal untuk menentukan luas daerah.

Soal 1. UN 2015
Luas daerah antara kurva $y=-x^{3}-x^{2}+2x$ dengan sumbu-(x) adalah ...
A. $\frac{40}{12}$ satuan luas
B. $\frac{39}{12}$ satuan luas
C. $\frac{37}{12}$ satuan luas
D. $\frac{29}{12}$ satuan luas
E. $\frac{15}{12}$ satuan luas

Pembahasan:
Langkah Pertama: Gambar kurva
Gambar kurva $y=-x^{3}-x^{2}+2x$ adalah sebagai berikut:

Langkah Kedua: Menentukan daerah yang akan dicari luasnya dan titik potong
Menentukan titik potong kurva $y=-x^{3}-x^{2}+2x$ dengan sumbu-(x), dengan cara mensubstitusi $y=0$ ke persamaan $y=-x^{3}-x^{2}+2x$. Titik potong ini digunakan untuk batas-batas integral.
$y=-x^{3}-x^{2}+2x$
$0=-x^{3}-x^{2}+2x$
$0=-x\left ( x^{2}+x-2 \right )$
$0=-x(x+2)(x-1)$
$x=0\ atau\ x=-2\ atau\ x=1$
Pembagian daerah beserta batas integral tersebut dapat dilihat dalam gambar berikut:

Langkah Ketiga: Mencari Integral dari setiap bagian tersebut
$L_1=\int_{0}^{1}{\left ( -x^{3}-x^{2}+2x \right )}\ dx$

$=\left [ -\frac{1}{4}x^{4}-\frac{1}{3}x^{3}+x^{2} \right ]\begin{matrix}1\\ \\ 0 \end{matrix}$
$=\left ( -\frac{1}{4}1^{4}-\frac{1}{3}1^{3}+1^{2} \right )-\left ( -\frac{1}{4}0^{4}-\frac{1}{3}0^{3}+0^{2} \right )$
$=-\frac{1}{4}-\frac{1}{3}+1$
$=\frac{5}{12}$

$L_2=-\int_{-2}^{0}{\left ( -x^{3}-x^{2}+2x \right )}\ dx$

$=-\left [ -\frac{1}{4}x^{4}-\frac{1}{3}x^{3}+x^{2} \right ]\begin{matrix}0\\ \\ -2 \end{matrix}$
$=-\left [\left ( -\frac{1}{4}0^{4}-\frac{1}{3}0^{3}+0^{2} \right )-\left ( -\frac{1}{4}(-2)^{4}-\frac{1}{3}(-2)^{3}+(-2)^{2} \right ) \right ]$
$=-\left [0-\left ( -4+\frac{8}{3}+4 \right ) \right ]$
$=\frac{8}{3}$

$Luas\ seluruhnya= L_1+L_2$

$=\frac{5}{12}+\frac{8}{3}$
$=\frac{37}{12}$

Jawaban: C

Soal 2
Luas daerah yang dibentuk oleh kurva $y=x^{2}-2x$ dan garis $y=2x$ adalah ...

Pembahasan:
Langkah Pertama: Gambar Grafik
Untuk mencari luas daerah yang dibentuk oleh dua kurva, kita menggambar kurva secara umum di bidang kartesius agar kita dapat membayangkan daerah yang mana yang harus kita cari luasnya. Kalau di gambar menurut kurva yang diberikan pada soal, maka akan seperti berikut:

Langkah Kedua: Memecah-mecah gambar serta menentukan titik potong kedua grafik
Yang dimaksud memecah-mecah gambar disini adalah membagi-bagi gambar menjadi beberapa bagian agar mudah meningtegralkan dan tidak menyalahi aturan dalam menentukan luas daerah integral.
Menentukan titik potong kedua kurva tersebut digunakan untuk mengetahui batas integral, dengan cara mensubstitusi kurva $y=2x$ ke kurva $y=x^{2}-2x$
$y=x^{2}-2x$
$2x=x^{2}-2x$
$x^{2}-4x=0$
$x(x-4)=0$
$x=0\ atau\ x=4$
Pembagian daerah beserta batas integral tersebut dapat dilihat dalam gambar berikut:

Langkah Ketiga: Mencari Integral dari setiap bagian tersebut
$L_1=-\int_{0}^{2}{x^{2}-2x}\ dx$

$=-\left [ \frac{1}{3}x^{3}-x^{2} \right ]\begin{matrix}2\\ \\ 0\end{matrix}$
$=-\left ( \frac{1}{3}2^{3}-2^{2} \right )-\left ( \frac{1}{3}0^{3}-0^{2} \right )$
$=-\left ( \frac{8}{3}-\frac{12}{3} \right )$
$=\frac{4}{3}$

$L_2=\int_{0}^{2}{2x}\ dx$

$=\left [ x^{2} \right ]\begin{matrix}2\\ \\ 0\end{matrix}$
$=2^{2}-0^{2}=4$

$L_3=\int_{2}^{4}\left ( f(x)-g(x) \right )\ dx$

$=\int_{2}^{4}\left ( 2x-\left ( x^{2}-2x \right ) \right )\ dx$
$=\int_{2}^{4}\left ( 4x-x^{2} \right )\ dx$
$=\left [ 2x^{2}-\frac{1}{3}x^{3} \right ]\begin{matrix}4\\ \\ 2\end{matrix}$
$=\left ( 2.4^{2}-\frac{1}{3}4^{3} \right )-\left ( 2.2^{2}-\frac{1}{3}2^{3} \right )$
$=32-8-\frac{64}{3}+\frac{8}{3}$
$=24-\frac{56}{3}$

Jadi Luas daerah yang dibentuk oleh kurva $y=x^{2}-2x$ dan garis $y=2x$ adalah
$Luas\ = L_1+L_2+L_3$

$=\frac{4}{3}+4+\left ( 24-\frac{56}{3} \right )$
$=\frac{32}{3}=10\frac{2}{3}$

Pembahasan Soal UN Garis Singgung

Soal 1, UN SMA Tapel 2017/2018 Program studi IPA
Persamaan garis singgung kurva $y=x^{2}-5x+12$ yang sejajar dengan garis $3x-y+5=0$ adalah ...
A. $3x-y+4=0$
B. $3x-y-4=0$
C. $3x-y-20=0$
D. $x-3y-4=0$
E. $x-3y+4=0$

Konsep dasar yang digunakan dalam perhitungan:

• Gradien garis singgung kurva $y=f(x)$ di titik $(x_1,y_1)$ adalah $m=f'(x_1)$, dengan $f'(x)$ turunan dari $f(x)$
• Persamaan garis singgung dengan gradien (m) dan sebuah titik $(x_1,y_1)$ adalah $y-y_1=m(x-x_1)$
• Persamaan garis $ax+by+c=0$ mempunyai gradien (m), dengan $m=-\frac{a}{b}$
• Dua garis dikatakan sejajar apabila gradiennya sama, yaitu $m_1=m_2$

Pembahasan
$3x-y+5=0$ mempunyai gradien $m_1=-\frac{3}{(-1)}=3$
Gradien garis singgung kurva $y=x^{2}-5x+12$ adalah $m_2=y'=2x-5$
Karena garis $3x-y+5=0$ sejajar dengan garis singgung kurva $y=x^{2}-5x+12$, maka gradiennya sama
$m_1=m_2$
$3=2x-5$
$8=2x\rightarrow x=4$
Untuk mencari (y), substitusi $x=4$ ke persamaan $y=x^{2}-5x+12$
$y=4^{2}-5.4+12$
$y=16-20+12$
$y=8$
Maka persamaan garis singgung kurva $y=x^{2}-5x+12$ mempunyai gradien $m_2=3$ dan melalui titik $(4,8)$
$y-y_{1}=m(x-x_{1})$
$y-8=3(x-4)$
$y-8=3x-12$
$y=3x-12+8$
$y=3x-4$
$3x-y-4=0$
Jawaban B

Soal yang sejenis

1. UN SMA Tapel 2017/2018 Program studi IPA
   Persamaan garis singgung grafik $y=x^{2}-4x-5$ yang sejajar dengan garis $2x-y-6=0$ adalah ...
   A. $2x-y-19=0$
   B. $2x-y-14=0$
   C. $2x-y-11=0$
   D. $2x-y+2=0$
   E. $2x-y+5=0$
   

Soal 1, UN SMA Tapel 2016/2017 Program studi IPA
Diketahui grafik fungsi $y=2x^{2}-3x+7$ berpotongan dengan garis $y=4x+1$. Salah satu persamaan garis singgung yang melalui titik potong kurva dan garis tersebut adalah ...
A. $y=5x+7$
B. $y=5x-1$
C. $y=x+5$
D. $y=3x-7$
E. $y=3x+5$

Pembahasan
Karena fungsi $y=2x^{2}-3x+7$ berpotongan dengan garis $y=4x+1$, maka kita perlu mencari titik potong kedua fungsi tersebut.
$2x^{2}-3x+7=4x+1$
$2x^{2}-7x+6=0$
$(2x-3)(x-2)=0$
$x_1=\frac{3}{2}\ atau\ x_2=2$
Substitusi $x_1=\frac{3}{2}$ dan $x_2=2$ ke persamaan $y=4x+1$

Untuk $x=\frac{3}{2}$ maka di dapat $y=4.\frac{3}{2}+1=7$. Jadi titiknya $(\frac{3}{2},7)$
Untuk $x=2$ maka di dapat $y=4.2+1=9$. Jadi titiknya $(2,9)$

$y=2x^{2}-3x+7 \mapsto y'=4x-3$
$x_1=\frac{3}{2} \mapsto m_1=y'=4.\frac{3}{2}-3=3$
$x_2=2 \mapsto m_2=y'=4.2-3=5$
Jadi terdapat dua garis singgung
Pertama garis singgung kurva yang melalui titik $(\frac{3}{2},7)$ dan mempunyai gradien 3
$y-y_1=m(x-x_1)$
$y-7=3(x-\frac{3}{2})$
$y=3x-\frac{9}{2}+7$
$y=3x+\frac{5}{3}$
Kedua garis singgung kurva yang melalui titik $(2,9)$ dan mempunyai gradien 5
$y-y_1=m(x-x_1)$
$y-9=5(x-2)$
$y=5x-10+9$
$y=5x-1$
Jawaban B

UN Matematika Program Studi IPS Tahun 2013
Diketahui fungsi $f(x)=\frac{2x-1}{3x-1}$. Turunan pertama fungsi $f(x)$ adalah $f'(x)$. Nilai dari $f'(1)=...$
A. -3
B. $\frac{1}{4}$
C. $\frac{1}{2}$
D. $\frac{2}{3}$
E. $\frac{5}{2}$
Pembahasan
Misal:
$u=2x-1$
$u'=2$
$v=3x-1$
$v'=3$
$f'(x)=\frac{u'v-uv'}{v^{2}}$
     $=\frac{2(3x-1)-(2x-1)3}{(3x-1)^{2}}$
     $=\frac{6x-2-6x+3}{(3x-1)^{2}}$
     $=\frac{1}{(3x-1)^{2}}$
$f'(1)=\frac{1}{(3.1-1)^{2}}=\frac{1}{4}$